저번에 정수의 덧셈에 대해서 알아보았고 곱셈과 나눗셈에 대해서 알아본다.
먼저 unsigned의 곱셈을 알아보도록 한다.
w-bit의 x와 y의 최대 최소값은 2^(w-1)~0이 된다. 그럼 두 수의 곱셈인 xy의 최대값은 2^2w - 2^(w+1) + 1~ 0이된다. 정리를 조금 해보자면
0 <= x,y <= 2^(w-1)
0 <= xy <= 2^2w - 2^(w+1) + 1
덧셈과 마찬가지로 xy의 결과는 원래의 비트인 w비트를 초과하고 원래대로 결과값을 가지기 위해선 2w비트가 필요로하다. 하지만 이도 마찬가지로 w비트를 늘릴수는 없으므로 overflow가 발생하게 된다. 정리하자면 w bit인 두 수가 곱셈을 진행했을 때 결과값은 2w비트의 값이 나오고 low order bit들만 저장하고 나머지 high order bit은 없어지게 된다.
그럼 예제는 조금 있다 살펴보고 2's complement수들을 살펴보겠다. 역시나 크기는 같은 조건 w비트에 signed 정수 x,y가 있을 때 x와y의 최소값, 최대값은 -2^(w-1), 2^(w-1)-1가 된다. 그리고 두 값의 곱 xy값의 최소값, 최대값은 각각 -2^(2w-2) + 2^(w-1), 2^(2w-2)가 된다. 정리해서 보자면
-2^(w-1)<= x,y <= 2^(w-1)-1
-2^(2w-2) + 2^(w-1) <= xy <= 2^(2w-2)
2's complement 상황에서도 2w비트가 필요하지만 low order bit만 저장하고 high order bit은 저장하지 않는다.

위의 예제로 계산이 어떤식으로 이루어지는지 살펴보자. 일단 x와 y는 3비트의 값이고 그 결과 역시 3비트로 저장되어야 한다. 첫번째 줄 unsigned에서 5와 3을 곱해서 결과값은 15가 나온다. 이진수로 표현했을 때 15는 [0011110]로 표현된다. 안타깝지만 high order bit 3자리는 생략이 되어 [111]만 저장되어 결국 7이 저장된다.
밑의 two's complement도 똑같은 원리이다. -3과 3이 곱해지면 -9이고 [110111]로 저장된다. 하지만 high order bit 3자리가 truncated 되어 [111]만 저장되어 -1값이 나온다. 나머지 예제도 똑같은 상황이니 설명을 더 이상 적지 않는다.
그리고 곱셈 부분에서 한가지 좀 특수한 상황을 살펴볼려고 한다. 바로 상수와 곱셈을 진행했을 때의 상황인데 그중에서도 2^k와 곱셈을 했을 때의 상황이다. x라는 수가 2^k와 곱셈을 진행을 할때 계산하는 방법은 x를 k비트만큼 왼쪽으로 swift하면 된다. 이건 unsigned 와 signed 둘다 적용된다. 그러면 일반 상수, 2^k이 아닌 수들도 2^k형식인 수로 각각 나뉘어 덧셈을 진행한다. 예를 들자면 x라는 수에 14을 곱하게 되면 14는 14 = 8 + 4 + 2이므로 x * 14 = (x<<3) + (x<<2) + (x<<1)처럼 진행이 된다. 이렇게 하는 이유는 곱셈은 clock cycle이 많이 필요로 하고 덧셈은 clock cycle이 적게 필요하기 때문이다. 덧셈, 뺄셈 그리고 shift하는 경우엔 일반적으로 1 clock cycle이 필요로하지만 곱셈은 10이상의 clock cycle이 필요하기 때문에 가급적 2^k식으로 표현이 가능한 상황에선 위 처럼 사용이 된다.
그럼 이어서 나눗셈에 대해서 얘기해보도록 한다. 나눗셈은 곱셈보다도 더 느리게 작동한다. 곱셈이 10개 이상의 clock cycle을 사용하기에 반면 나눗셈은 30 clock cycle이상이 필요로 하다.
x를 2^k로 나누었을 때는 x를 k만큼 오른쪽으로 logical shift해주면 결과값이 나온다.
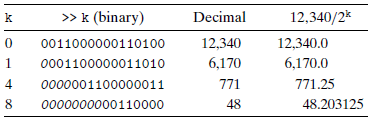
logical shift는 없어진 비트를 없어진 비트와 상관없이 0으로 채우는 shift이다. 위의 예시들에는 그럼 예시들이 없지만 logical shft를 하게 되면 소수점의 크기와 상관없이 0으로 가까운쪽으로 결과값이 생략된다. 이러한 생략을 round toward 0라고 부른다.
이어서 signed x가 2^k으로 나누었을때 똑같이 오른쪽으로 k만큼 arithmetic swift하게 된다. arithmetic swift는 없어진 비트에서 제일 가까운 비트로 늘어나는 것이다. 그 이유는 signed의 제일 왼쪽 비트, MSB비트가 sign비트이기 때문이다.
여기서 x가 음수 일땐 조금 문제가 발생한다.

앞에서 말한대로 k만큼 오른쪽으로 swift하게 된다면 결과값은 원래 값보다 더 작게 된다. 위의 표에서 k가 4와 8일때를 살펴보면 k가 4일때 원래 값은 -771.25이지만 -772가 된다. 그리고 이 값은 0이란 값에서 더 멀어지게 된다. 양수일 때는 0과 가까이 되는데 음수일때는 멀어진다? 이것이 허락되지 않아 결국 이를 0으로 가까운값으로 가도록 통합시키게 된다. 그래서 지금 상황에서 이를 보정하는 방법은 x/2^k를 (x+2^k-1) / 2^k로 계산하게 되면 0쪽으로 가까운 수로 결과가 나오게 된다.

위의 표에서 그 결과를 보여주고 있다. (x+2^k-1) / 2^k 이 공식은 뭐 조금만 수학적으로 생각해보면 우리가 원하는 값이 나오겠다라고 생각이 들겠다.
'시스템프로그램' 카테고리의 다른 글
| [시스템프로그램]02-3-2 실수와 사칙연산(2) (0) | 2020.04.30 |
|---|---|
| [시스템프로그램]02-3-1 실수와 사칙연산(1) (2) | 2020.04.29 |
| [시스템프로그램]02-2-1 정수의 사칙연산(1) (0) | 2020.04.27 |
| [시스템프로그램]02-1-3 정보의 표현과 활용(3) (2) | 2020.04.26 |
| [시스템프로그램]02-1-2 정보의 표현과 활용(2) (2) | 2020.04.20 |




댓글